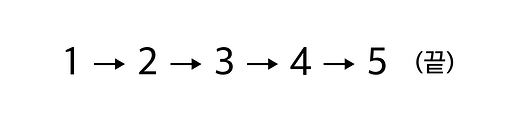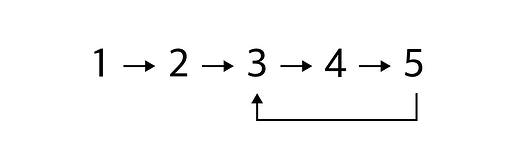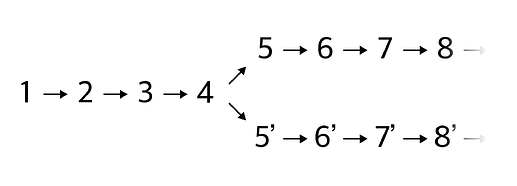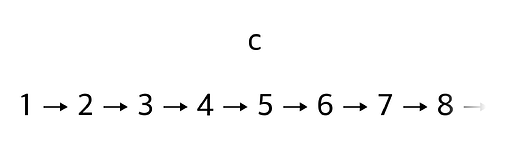어느 날 디멘은 외계인을 만났습니다. 외계인이 디멘에게 물었습니다. "인간들이 사용하는 개념 중에서 도저히 이해되지 않는 게 있어. 도대체 자연수가 뭐야?"
"뭐긴 뭐야. 자연수란 1부터 시작해서 2, 3, 4, … 이렇게 순서대로 나아가는 수 체계야." 디멘의 대답에 외계인이 다시 물었습니다. "음…그러면 이것도 자연수야?"
"엥? 그럴 리가! 자연수는 끝없이 이어져." 그러자 외계인이 다시 물었습니다. "끝없이 이어진다고? 고리를 이룬다는 말인가? 그럼 1, 2, 3, 4, 5, 3, 4, 5, 3, 4, 5, … 이렇게 끝없이 이어지는데."
디멘은 기겁했습니다. "맙소사, 그 뜻이 아니야. 고리 같은 거 없이 끝없이 이어져." 그러자 외계인이 갸우뚱거렸습니다. "흠...그럼 중간에 가지라도 치나?"
디멘은 슬슬 화가 나기 시작했습니다. "그것도 아니야! 가지는 없어!" 하지만 외계인은 아랑곳하지 않고 물었습니다. "알겠어. 그렇다면 혹시 c도 자연수니?" "c라니, 무슨 말이야?" "너가 알려준 자연수의 정의대로라면 c가 자연수가 아닐 이유는 없는데? 자연수는 끝없이 이어진다고 했지만 모든 자연수가 그러한 연쇄의 일부라고 말하지는 않았잖아."
"저건 또 뭐야!! 자연수에는 자연수밖에 없어!!" 이 말에 외계인은 퉁명스럽게 말했습니다. "자연수에는 자연수밖에 없다니, 순환논법이 따로 없네." 이제 디멘은 정말로 화가 났습니다. "너 지금 나 놀리는 거지?" "무슨 소리야. 난 진짜 자연수가 뭔지 모르겠어. 너야말로 자연수의 정의를 제대로 알려줘야 내가 이해를 할 거 아니야." 하지만 디멘은 답답해 미칠 지경이었습니다. "자연수란...음...그러니까...하, 이걸 어떻게 설명하지!!"
그 순간, 데데킨트라는 사람이 나타났습니다. "내가 이 문제를 확실히 해결해 주지. 자연수란 다음 네 가지 조건을 만족하는 집합을 말해. 이 네 가지 조건을 만족하는 집합이 유일하다는 사실은 내가 증명해 놓았으니 더 이상 오해의 여지라고는 없지!"
데데킨트의 대답에 외계인은 흡족해했지만, 이내 또다시 의아하다는 표정을 지었습니다. "네 번째 조건에 '임의의 명제'라는 표현이 말이 돼? P(x)가 임의의 명제라면 P(x)는 'x가 자연수이다'가 될 수도 있잖아. 하지만 자연수의 정의에 자연수에 대한 명제가 포함되는 건 순환논법일 텐데?" 뜻밖의 지적에 데데킨트가 우물쭈물하자 옆에서 뢰벤하임이라는 사람이 끼어들었습니다. "확실히 '임의의 명제'라는 표현은 문제가 있어 보이네. 아무래도 수학에서 이런 표현은 제한해야겠어. 이렇게 제한된 논리학을 1차 논리라고 부르자."
데데킨트가 말했습니다. "그렇다면 이제 어떻게 1차 논리로 자연수를 정확하게 정의할 수 있는지 알아봐야겠군." 이 말에 스콜렘이라는 사람이 불쑥 나타났습니다. "맞아. 그리고 내가 이 질문에 대한 답을 발견했어." 스콜렘의 발언에 모두가 주의를 집중했습니다.
"불가능해." 스콜렘이 말했습니다. "1차 논리로는 자연수의 필요충분조건을 기술할 수 없어. 구체적으로, 자연수가 어떤 1차 논리 문장을 만족한다면 자연수가 아니면서 그 문장을 만족하는 대상이 언제나 존재해. 그러니까, 자연수는 순환논법 없이 정의할 수 없어."
순간 정적이 흘렀습니다. 외계인이 물었습니다. "그렇다면 인간들은 어떻게 자연수가 뭔지 아는 거야? 알고 보면 인간들은 저마다 자연수를 다르게 알고 있는 거 아냐?" 외계인의 질문에 아무도 대답하지 못했습니다.
그들은 신기루 같은 자연수의 실체에 대해 할 말이 더 이상 남아 있지 않았습니다.
Note. 이야기의 자연스러운 흐름을 위해 왜곡된 역사적 · 수학적 · 철학적 내용이 있습니다. 1차 논리의 탄생은 뢰벤하임을 비롯한 여러 수학자들의 점진적인 연구로 이루어졌습니다. 또한, 데데킨트의 자연수 정의, 즉 2차 논리가 정말로 순환적인지에 관해서는 더 자세한 논의가 필요합니다. 또한 스콜렘의 역설은 자연수에 관한 것이 아닌 집합론에 관한 것인데, 뢰벤하임-스콜렘 정리의 귀결이라는 점에서 두 현상은 유사하기 때문에 말풍선에 넣었습니다.