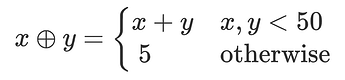수학에서 크립키의 역설에 대한 생각

잡념
1

크립키의 역설은 규칙 따르기의 상대성을 보이기 위해서 제시한 역설로, 모든 수학적 정의와 규칙은 과거 사례를 관찰하는 방식만으로는 미래에도 정확히 적용할 수 없다고 확신할 수 없다고 말합니다.
하지만, 제 생각에 크립키의 역설은 수학의 체계의 불건전성(부정 가능성)을 보일 수 있는 역설이 아닙니다.

크립키는 어떤 기호가 유한한 적용사례로부터 무한한 적용대상을 정당화 할 수 없기 때문에 기호가 불분명하다고 말합니다.
예를 들어, quus라는 연산은

image
image834×194 10.8 KB

라고 합니다. 누군가에게 이제까지 수행한 덧셈이
quus가 아닌 것을 보일 수 없다고 주장할 수 있습니다. 50이상의 값에 대해 일반적으로 연산우해보지 않았기 때문입니다.

하지만 덧셈은 무한한 입, 출력 쌍으로부터 정의된 것이 아니기 때문에 이전까지의 연산사례로부터 덧셈을 정당화할 필요가 없습니다. 정의된 바에 따라 모든 입력에 대해 적용하면 그만입니다. 물론, 위 사례는 하나의 예시일 뿐이고, 계속 그 정의를 추적해서 크립키의 역설을 적용한다면 결국 공리, 무정의 용어에 도달할 것입니다.

일반적인 현대수학에서 사용하는 무정의 용어는 '집합'과 '포함관계'이고, 공리계는 'ZFC 공리계'입니다. 수학에 흠을 내기 위해서 이들에 quus와 같은 것을 생성할 수 있을까요?

여기서 주의해야할 점은 ZFC 공리계에 모순되지 않는 꼴로 생성해야 한다는 것입니다. 크립키의 역설은 기호의 불확실성을 논하는 것이 목적이지, ZFC 공리계의 비직관성을 논하고자 하는 것이 아니기 때문입니다.

또한, 집합과 포함관계를 새로이 '정의'해서는 안됩니다. 왜냐하면, 수학 체계는 애초에 집합과 포함관계를 특별히 정의하고 있지 않기 때문입니다. 마치 허수아비를 때리는 것과 같은 것입니다.

결과적으로 그렇습니다, ZFC 공리계의 완성입니다. 집합과 포함관계에 대해 추가적인 정의를 내릴수도, ZFC 공리계에 대해서도 모순을 발생시킬 수 없기 때문에 애초에 크립키의 역설은 수학 체계에 변화를 일으킬 수 없습니다.

다른 접근으로, ZFC 공리계에 모순되지 않으면서 집합과 포함관계에 새로운 성질을 추가할 수 있습니다. 그렇다면 다양한 해석이 가능한 것이라고 주장할 수 있겠습니다.

이것은 매우 중요한 접근이고, 실제 그런 사례가 있습니다. 바로 연속체 가설입니다. 연속체 가설이 참이든 거짓이든 ZFC 공리계와 어떠한 모순이 일어나지 않음이 증명되었습니다. 즉, 연속체 가설의 결과에 따라 집합과 포함관계에 대한 미묘한 해석 변화가 생겼다고도 할 수 있습니다.

하지만 이것은 문제가 되지 않습니다. 왜냐하면, 그러한 문제에 대해서 ZFC 공리계 하의 논의에서는 '알 수 없다'로 말하기 때문입니다. 애초에 그러한 것들은 관심 대상이 아닌 것입니다. 애초에 그것에 대해서는 참, 거짓을 주장하지도 않습니다. 덧셈의 모든 입출력 관계를 주장하는 것과는 상반되는 일입니다. 하지만 말 그대로 ZFC공리계와 모순을 만들지 않으면서 결정되지 않은 성질들은 '주장 대상'이 아닙니다.

그런 사례는 아주 다양합니다. 예를 들어, 유클리드 5공리에서 평행선 공준을 제외하면 쌍곡기하, 구면 기하 등의 다양한 해석이 나타납니다. 하지만, 평행성 공준 하에서는 평면기하만 나타날 뿐입니다.

즉, 크립키의 역설이 수학계에서 보이는 실체는 사실 '허수아비 공격'일 뿐인 것입니다.

+) ZFC 공리계에 사용되는 또다른 무정의 용어 '모든($\forall$)'과 '존재함($\exists$)'에 대해서도 크립키의 역설을 적용해볼 수 있을 것입니다. 예를 들어, 사실 '모든'이란 것이 '방금 제가 떠올린 것'를 뺀 모든이었다던가...(모두들 '방금 제가 떠올린 것'에 대해서 적용해본 적이 없을 것이므로)

약간의 유머이고, 의미없는 적용임을 다들 아실 것입니다.

수학의 불건전성을 보일 수 있는 것은 크립키의 역설을 말고 아주 강력한 것이 있습니다. 괴델의 제2 불완전성 정리에 따르면, 어떤 공리체계는 자신 내부에서 그 무모순성을 증명할 수 없습니다. 그러니까, 사실 ZFC 공리계에도 모순이 있는데 아직 사람들이 발견 못 한 것일 수 있습니다. 즉, 부정 가능성이 있는 것입니다. 하지만, ZFC 공리계는 충분히 직관적이고 단순하기 때문에 모순을 생각하기 쉽지 않습니다.

1개의 좋아요
2

이 부분이 크립키의 역설이 말하는 핵심에서는 어긋나 있는 것 같습니다. 크립키는 (a) “덧셈이란 무한한 입, 출력 쌍으로 ‘정의된다.‘“라고 주장한 것이 아니라 (b) “당신이 덧셈에 대해 어떠한 엄격한 정의를 제시하든지, 그 정의를 만족시키면서도 우리의 통념과는 ‘완전히 다른 방식으로 덧셈을 해석하는 것이 가능하다.‘“라고 주장하는 것입니다. (가령, quus는 우리가 제한된 상황에서 plus에 대한 일상적 정의나 설명이라고 생각하는 모든 요소들을 만족시키면서도, plus와는 완전히 다른 방식으로 이루어지는 계산법이라는 점을 염두에 두시면 좋을 것 같습니다. 이러한 사례를 얼마든지 모든 종류의 상황으로 확장할 수 있다는 것이 크립키의 논지입니다.)

그리고 이러한 크립키의 문제제기와 관련해서, 글 속에서 다소 애매하게 쓰인 부분들이 있는 것 같습니다. 크립키의 논점을 비판하는 것인지 옹호하는 것인지 저에게는 분명하지 않아 보이는 부분들이 있어서요. 가령,

이 주장은 (a) 공리나 무정의 용어로 엄격한 정의를 제시하는 것이 가능하다는 의미로 쓰신 건가요, 아니면 (b) 공리나 무정의 용어 그 자체에 대해서 크립키의 역설이 다시 적용 가능하다는 의미로 쓰신 건가요. 크립키는 후자의 주장을 하고 있는 것이다 보니, (그래서 우리가 정의할 필요조차 없는 용어라고 생각하는 것조차도 통념과 완전히 다른 의미로 해석하는 것이 가능하다고 지적하는 것이다 보니,) (a)라면 크립키의 논점과 어긋나는 이야기로 읽히고, (b)라면 크립키의 논점을 옹호하는 이야기로 읽힙니다. 또한

이 부분도 마찬가지입니다. (a) ‘모든‘과 ‘존재한다‘라는 무정의 용어들에 대해서는 크립키의 역설이 적용될 수 없다는 의미로 쓰신 것인지, (b) 그 용어들에도 크립키의 역설이 얼마든지 적용될 수 있기 때문에 ZFC 공리계로 덧셈을 정초하려는 시도조차 엄격한 철학적 관점에서는 근거가 없다는 것인지 불분명합니다. 덧붙이자면, 실제로 메타형이상학에서는 ‘존재한다‘라는 표현이 일의적인 의미를 지니는지 다의적인 의미를 지니는지에 대한 논쟁들이 있고, 그와 관련해서 어떠한 개체가 ‘모든‘이라는 양화사로 지칭될 수 있는지도 이론에 따라 얼마든지 달라질 수 있습니다.

7개의 좋아요
3

크립키의 역설은 수학적 확실성을 공격하고 있는 것이 전혀 아니고, "의미"의 확실성을 공격하고 있는 것입니다. 따라서 덧셈이라는 규칙이 어떠한 비판도 허용하지 않는 완전무결한 규칙이라고 인정한다고 하더라도, 크립키의 역설은 여전히 발생한다고 크립키가 주장하고 있는 것입니다. 즉 핵심은 덧셈이라는 완전무결한 수학적 규칙이 있다고 했을 때,

너가 지금까지 "+"를 (quus규칙이 아닌) 바로 그 완전무결한 덧셈규칙으로 의미했다는 사실을 어디에서 알 수 있느냐?

에 대한 것입니다. 이 점이 다음의 문단에서도 잘 나타납니다.

The problem is not "How do I know that 68 plus 57 is 125?", which should be answered by giving an arithmetical computation, but rather "How do I know that '68 plus 57', as I meant 'plus' in the past, should denote 125?" If the word 'plus' as I used it in the past, denoted the quus function, not the plus function (,quaddition' rather than addition), then my past intention was such that, asked for the value of'68 plus 57', I should have replied '5'· - [Wittgenstein on Rules and Private Language (1984), 12쪽.]

9개의 좋아요
4

상세사항에서야 물론 다릅니다만, 유사한 의미 미결정성이란 측면에서는 링크된 멋진 만화 또한 이해에 도움이 되실듯 합니다.

6개의 좋아요
5

Herb님이 잘 지적하신 것처럼 (제가 알기로는) 크립키는 자신의 규칙따르기 역설을 "수학의 체계의 불건정성(부정 가능성)"을 보이는 것으로 생각한 적이 없으며 규칙따르기 역설이 그러한 귀결을 갖는다고 주장한 철학자도 없는 것 같습니다. 크립키가 보이려고 하는 것은 한글단어 '덧셈'이 수학에서 말하는 덧셈을 의미한다는 의미-사실이 존재하지 않는다는 것입니다. 덧셈에 대해 수학이 말하는 어떠한 내용에 대해서도 크립키의 규칙따르기 역설이 시사하는 바는 없습니다. 이 역설이 함축하는 것은 한글단어 '덧셈' 혹은 영어 단어 'plus' 혹은 기호 '+'가 수학에서 말하는 연산으로서의 덧셈을 의미한다는 사실이 존재하지 않는다는 것입니다.

4개의 좋아요
6

@Herb 님과 @mimmum 님이 잘 말씀해 주신 것처럼 크립키의 회의적 역설은 분명히 '의미 회의주의'를 주장하고 있는 것이 맞습니다. 다만, 의미 회의주의가 수학에 대해 아무것도 시사하는 바가 없다는 @mimmum 님의 주장은 약간 과한 바가 있지 않은가 합니다. 애초에 '규칙 따르기'라는 논의는 비트겐슈타인의 수학철학의 맥락에서 제시된 논의입니다. (덧붙이자면, 비트겐슈타인은 자신의 가장 중요한 철학적 성과가 수학철학에 있다고 스스로 평가하였습니다.) 또한 크립키 역시 이 논의를 수학의 연산과 연관시켜서 해명하고 있죠.

그래서 저는 (a) '규칙 따르기'와 '회의적 역설'이 그 자체로는 '의미'라는 주제를 중심으로 벌어지는 논의라는 것은 분명하지만, (b) '의미'라는 주제가 '수학'이라는 주제보다도 훨씬 더 근본적이고 포괄적인 주제라는 점에서, (c) 회의적 역설은 의미론에 국한된 지엽적 문제를 넘어서 분명히 수학에 대한 철학적 시사점까지도 아주 풍부하게 함의하고 있다고 봅니다. 우리가 사용하는 언어의 '의미'를 보장해줄 만한 어떠한 초사실도 존재하지 않는다는 회의적 역설의 논의대로라면, 당연히 수학에서 사용되는 개념, 정의, 공리, 연산 등의 '의미'를 보장해 줄 만한 초사실도 존재하지 않는 것이 되고, 이러한 회의는 수학 자체가 사실은 아무런 형이상학적 토대가 없는 상태에서 성립한 학문이라는 주장를 함의하고 있는 것이니 말입니다. 구체적으로는, 크립키가 잘 지적하고 있는 것처럼, 68+57로부터 125를 도출해야 하는지 5를 도출해야 하는지를 확고하게 결정해 줄 만한 아무런 토대도 없다는 것이 분명히 회의적 역설이 함의하고 있는 사실이죠.

*염려가 되어서 덧붙이자면, 규칙 따르기나 회의적 역설은 수학계 내부의 고민이나 논쟁에 대해 어떠한 시사점을 주고 있는 논의가 당연히 아닙니다. 가령, 회의적 역설을 받아들인다고 해서 우리가 ZFC 공리계를 거부해야 하거나, 뢰벤하임-스콜렘 정리가 새로운 방식으로 조명될 수 있거나 하는 것은 전혀 아니죠. 하지만 이 논의는 수학에 대한 '철학적' 해석에는, 다시 말해 '수학철학'에는 시사점을 주고 있는 논의가 맞습니다. 수학에서 너무나 자명하게 이루어지는 실천들을 보장해 줄 만한 '실재'나 '인과'나 '성향' 따위가 없다고 강조한다는 점에서, 회의적 역설은 수학에 대한 반실재론을 지지하는 논증으로 충분히 읽힐 수 있죠.

7개의 좋아요
7

크립키의 역설이 ‘덧셈’을 사례로 들고 있지만 수학 언어의 표현을 사용하는 것이 그의 논증에 필수적인 것은 아닙니다. 크립키도 이를 명시적으로 지적했던 것으로 기억합니다. (비트겐슈타인은 제가 잘 모릅니다.) 물론 의미 사실에 대한 반실재론은 수학 언어의 표현들의 의미 사실들에 대한 반실재론을 사소하게 함축할 것입니다. 이러한 의미에서 물론 크립키의 역설이 수학에 대해 어떤 함의를 가질 수는 있겠습니다. 제가 의도했던 것은 이런 사소한 함의가 아닌, 수학 철학에 대해 특별히 크립키의 역설이 함의하는 바가 없다는 점이었습니다.

그런데 저는 다음과 같은 @YOUN 님의 주장에 대해서는 반대합니다.

블록 따옴표 우리가 사용하는 언어의 '의미'를 보장해줄 만한 어떠한 초사실도 존재하지 않는다는 회의적 역설의 논의대로라면, 당연히 수학에서 사용되는 개념, 정의, 공리, 연산 등의 '의미'를 보장해 줄 만한 초사실도 존재하지 않는 것이 되고, 이러한 회의는 수학 자체가 사실은 아무런 형이상학적 토대가 없는 상태에서 성립한 학문이라는 주장를 함의하고 있는 것이니 말입니다. 구체적으로는, 크립키가 잘 지적하고 있는 것처럼, 68+57로부터 125를 도출해야 하는지 5를 도출해야 하는지를 확고하게 결정해 줄 만한 아무런 토대도 없다는 것이 분명히 회의적 역설이 함의하고 있는 사실이죠.

@YOUN 님은 "우리가 사용하는 언어의 '의미'를 보장해줄 만한 어떠한 초사실도 존재하지 않는다는 회의적 역설의 논의대로라면, 당연히 수학에서 사용되는 개념, 정의, 공리, 연산 등의 '의미'를 보장해 줄 만한 초사실도 존재하지 않는 것"이 된다고 말씀하셨습니다. 이는 '개념,' '정의,' '공리,' '연산,'을 의미를 갖는 혹은 의미를 갖는 것으로 대체로 간주되는 언어적 존재자로 취급하고 있습니다. 앞서 말한 것처럼 크립키의 역설은 이러한 언어적 존재자들이 갖는 의미에 대한 의미 사실들이 존재하지 않는다는 점을 수학 표현이 아닌 표현들, 예를 들어 과학 표현들의 의미 사실이 존재하지 않는다는 점을 함축하는 것과 같이 사소하게 함축합니다.

하지만 왜 "이러한 회의는 수학 자체가 사실은 아무런 형이상학적 토대가 없는 상태에서 성립한 학문이라는 주장"이 함의되는지 모르겠습니다. 수학적 대상들에 대한 플라톤주의는 수학 표현들이 의미를 갖지 않는다고 하더라도 참일 수 있습니다. 물론 수학 표현의 의미에 대한 사실이 없다면 플라톤주의의 동기 중 하나를 잃을지도 모르겠습니다 - 수학적 진술의 의미에 대한 분명한 설명을 제공한다는 것을 플라톤주의의 동기로 삼는다는 가정하에 말입니다. 하지만 이러한 동기가 플라톤주의가 갖는 유일한 동기는 아닙니다. 수학적 사실의 필연성과 수학적 지식의 선험성에 대한 설명력 또한 플라톤주의의 동기가 될 수 있기 때문입니다.

저는 "68+57로부터 125를 도출해야 하는지 5를 도출해야 하는지를 확고하게 결정해 줄 만한 아무런 토대도 없다는 것이 분명히 회의적 역설이 함의하고 있는 사실"이 아니라고 생각합니다. 회의적 역설이 함의하고 있는 사실은 반대로 '68+57가 무엇입니까?'에 대한 올바른 대답이 '125'인지 아니면 '5'인지를 결정해줄 토대가 없다는 사실입니다. 이러한 사실은 68 +57이 125인지 5인지 여부를 결정해줄 사실이 없기 떄문이 아니라 '68+57이 무엇입니까?'에서 '+'가 plus를 의미하는지 quus를 의미하는지를 결정해줄 사실이 없기 때문입니다. 수학적 사실은 수학적 표현의 의미사실이 없다 하더라도 존재한다고 생각하는 것이 가능합니다. 이는 '+'가 plus를 의미할 경우 우리는 '68+57이 무엇입니까?'에 대한 올바른 대답이 '125'라는 점으로부터 보여집니다.

5개의 좋아요
8

논의에 여러 가지 층위가 걸려 있는 것 같습니다. 우선, @JarOfDesire 님의 원글에서 '수학'과 '수학철학'의 층위가 다소 혼동되어 있기도 하고, @mimmum 님과의 댓글에서는 크립키의 회의적 역설이 '수학철학' 내부에서 어떠한 함의를 지니는지에 대해 다소 의견이 갈리네요. 제 관점에서 전체적인 이야기의 흐름을 정리해 보면서 대답을 해보고 싶습니다.

(1) 수학과 수학철학: 불건전성, 불완전성, 부정가능성은 서로 같은 의미가 아니다.

@JarOfDesire 님의 혼동은 우선 여기에서 발견됩니다. 다른 분들이 잘 강조해 주신대로, 크립키의 역설은 그 자체로는 논리학이나 수학에서 말해지는 '불건전성(unsoundness)'이나 '불완전성(incompleteness)'과는 아무런 상관이 없습니다. 저도 댓글에서 지적하였지만, 크립키의 역설을 받아들인다고 해서 ZFC 공리계가 무너지지도 않고, 뢰벤하임-스콜렘 정리나 괴델의 제2불완전성 정리 등이 새롭게 뒷받침되는 것도 아닙니다.

비트겐슈타인이나 크립키가 보여준 것은, 우리가 특정한 암묵적 배경 속에서만 덧셈 규칙을 자명하고 확고하게 따를 수 있다는 것입니다. 비트겐슈타인에게는 그 배경이 '삶의 형식'과 '자연사'였고, 크립키는 '공동체'였다는 차이가 있지만, 그 둘 모두에게서 핵심은 수학이 모종의 '인류학적' 배경에 호소하지 않고서는 그 자체로 성립하는 규칙 따르기가 아니라는 점입니다. 그래서 @wildbunny 님이 댓글로 올려주신 @dimen 님의 만화에서 나오는 것처럼, 우리 인간과 완전히 다른 방식으로 살아가면서 사고하는 외계인에게는 덧셈은 커녕 자연수가 무엇인지조차 설명이 안 된다는 것이죠.

크립키의 회의적 역설이 수학에 대한 '부정가능성'을 지니는 지점이 있다고 한다면, 바로 이러한 지점이라고 할 수 있습니다. 수학 자체만의 사유 속에 갇힌 사람, 다시 말해 수학 자체에 대해 한 번도 철학적으로 성찰해 보지 않은 사람, 그래서 '자연수'나 '덧셈' 같은 아주 자명하고 확실한 것처럼 보이는 수학의 개념들조차도 언제든지 완전히 의문에 빠질 수 있다는 사실을 자각하지 못한 사람에게는, 크립키의 회의적 역설이 마치 수학 자체를 완전히 무너뜨리는 힘을 지닌 것처럼 보일 수도 있습니다. 그래서 저는 크립키의 회의적 역설을 수학의 내적 관점에서 극복해 보고자 하는 @JarOfDesire 님의 시도가 아주 이해가 되지 않는 것은 아닙니다.

다만, @JarOfDesire 님의 시도가 방향이 잘못 잡혀 있는 것은, 크립키의 역설이 바로 @JarOfDesire 님이 의존하고 있는 공리계 자체의 '의미'를 문제 삼는다는 점입니다. 제가 짐작하는 것이 맞다면, @JarOfDesire 님은 무정의 용어와 같은 것의 의미에 대해 고민하는 것이 "약간의 유머이고, 의미없는 적용"이라고 생각하시는 것 같지만, 오히려 비트겐슈타인이나 크립키는 @JarOfDesire 님이 무시해버리는 그 지점이 '철학적'인 지점이라고 지적하고 있는 셈입니다. 수학자들은 특정한 암묵적 배경을 아주 자명하고 확실하게 받아들인 상태에서 '수학계' 혹은 '수학장' 내부에서만 논의를 전개하지만, 그래서 그 내부에서는 수학이 더 이상 의심할 수 없는 확실성을 지닌 것으로 성립하지만, 비트겐슈타인이나 크립키는 단순히 수학자들이 그 암묵적 배경에서 "그렇게 하고 있을 뿐"(PI, §217)이라고 말하면서, 수학 바깥에서 수학을 성찰하고 있는 것입니다.

(2) 수학철학: 회의주의와 플라톤주의

그래서 비트겐슈타인과 크립키의 논의가 단순히 '수학' 내부에서가 아니라 '수학철학'이라는 지평에서 이루어지는 논의라고 한다면, 이들의 논의가 과연 수학철학에서 어떠한 함의를 지닐 수 있을지가 다시 논쟁의 대상이 될 수 있겠죠. 여기서 @mimmum 님과 저 사이에 다소 해석의 차이가 있는 것 같습니다. 그런데 우선,

저는 이 주장 자체에 대해서는 반대하지 않습니다. 제 기억상으로도, 크립키가 반드시 수학이라는 주제를 겨냥하여 회의적 역설을 제시하지는 않았습니다. 그래서 크립키의 회의적 역설이 수학철학에서 어떠한 함의를 지니는지는, 단순히 크립키의 텍스트 자체만으로 평가할 수 있는 문제가 아니라, 크립키의 텍스트에 대한 철학적 해석과 연구를 동반하는 문제가 될 것입니다. (다만, 비트겐슈타인의 경우 스스로 수학철학에 상당한 의의를 두었다는 점은 몽크의 Ludwig Wittgenstein: The Duty of Genius 149쪽 등에서 확인됩니다. 물론, 이 경우조차 비트겐슈타인의 수학철학이 비트겐슈타인 자신이 생각한 것만큼 의의가 있는지에 대해서는 논쟁이 있을 수 있고, 실제로도 크라이슬, 퍼트남, 더밋처럼 비트겐슈타인의 수학철학을 그다지 높이 평가하지 않는 인물들도 있지만 말입니다.)

다만, 크립키가 일반적인 의미의 '플라톤주의'에 대해 부정적으로 평가하고 있다는 점은 텍스트상으로도 확인됩니다. 물론, 여기서 플라톤주의가 반드시 '수학적 실재에 대한 플라톤주의'인 것은 아니지만, 플라톤주의에 대해 크립키의 비트겐슈타인이 취하는 태도는 수학적 실재에 대한 플라톤주의로도 얼마든지 적용될 수 있을 것입니다.

For Wittgenstein, Platonism is largely an unhelpful evasion ofthe problem of how our finite minds can give rules that are supposed to apply to an infinity of cases. Platonic objects may be selfinterpreting, or rather, they may need no interpretation; but ultimately there must be some mental entity involved that raises the sceptical problem. (This brief discussion of Platonism is meant for those interested in the issue. Ifit is so briefthat you find it obscure, ignore it.)

S. Kripke, Wittgenstein on Rules and Private Language, Cambridge, Massachusetts: Harvard University Press, 1982, p. 54.

물론, 이 구절 자체가 수학철학에 대한 크립키의 입장을 보여주지는 않습니다. 또한 @mimmum 님이 적절하게 지적하신 것처럼,

이렇게 의미 회의주의의 문제와는 전혀 다른 동기에서 플라톤주의가 성립하는 길도 남아 있을 수 있습니다. 저는 이러한 @mimmum 님의 주장 자체를 부정하지는 않습니다. 다만, 크립키의 회의적 역설은 플라톤주의에 대한 거부를 적어도 텍스트상에서만큼은 실제로 담고 있고, 또 그 거부가 수학철학의 플라톤주의에 대한 거부와 이어질 수 있는 여지가 많다는 것이 저의 주장일 뿐, 다른 관심과 목적을 지닌 플라톤주의가 성립할 수 있을지도 모른다는 주장까지 잘못되었다고 생각하지는 않습니다. 다만,

이 부분이 정확히 무엇을 의미하는지 저로서는 완전히 이해되지는 않습니다. 우선 (a) "68+57로부터 125를 도출해야 하는지 5를 도출해야 하는지를 확고하게 결정해 줄 만한 아무런 토대도 없다"와 (b) "'68+57가 무엇입니까?'에 대한 올바른 대답이 '125'인지 아니면 '5'인지를 결정해줄 토대가 없다"라는 두 문장이 본질적으로 다른 문장인지 분명하지 않습니다. 또한

라는 주장은 오히려 비트겐슈타인의 본래 주장에 가깝기도 합니다. '초사실' 따위가 존재하지 않는다고 하더라도 '수학적 사실'이 얼마든지 존재할 수 있다는 것이 비트겐슈타인의 주장이라고 저는 이해하고 있고, 마르틴 쿠쉬 같은 학자는 심지어 크립키의 회의적 역설을 이와 유사한 방식대로 해석하기도 합니다. 그래서 저는 @mimmum 님이 쓰신 마지막 문단의 의미가 다소 저에게는 불확실하다는 점만 제외하면, 저와 @mimmum 님의 주장 사이에 큰 차이가 있는지 잘 모르겠습니다.

5개의 좋아요
9

논의를 계속해주신 @YOUN 님께 감사드립니다.

먼저 제 원래 댓글에서 '수학적 대상들에 대한 플라톤주의'라고 한 것처럼 제가 염두에 둔 플라톤주의는 수학철학에서 말하는 플라톤주의입니다. @YOUN 님께서도 이야기하신 것처럼 수학철학의 플라톤주의는 크립키가 인용하신 부분에서 언급하는 플라톤주의와는 다른 것처럼 보입니다. 제가 지금 책이 없어서 앞뒤 문맥을 확인할 수 없는데 인용문만 보자면 여기서의 플라톤주의는 규칙에 대한 플라톤주의인 것처럼 읽힙니다. 규칙에 대한 플라톤주의와 수학철학의 플라톤주의는 몇가지 중요한 점에서 다르기 떄문에 규칙에 대한 플라톤주의에 대한 반감이 수학철학의 플라톤주의에 대한 반감으로 자연스럽게 확장될 수 있는지 여부는 분명하지 않습니다. 한가지 중요한 차이점만 언급하자면 규칙은 우연적이고 수학적 대상들은 필연적이라는 차이가 있습니다. 우연적 존재자인 것처럼 보이는 규칙에 대한 플라톤주의는 필연적 존재자인 수학적 대상들에 대한 플라톤주의와는 그 설득력에 있어서 큰 차이를 가질 것처럼 보입니다.

더불어 인용문을 볼 때 최소한 저에게는 크립키가 규칙에 대한 플라톤주의를 거부하는 것처럼 읽히지는 않습니다. 크립키는 여기서 규칙에 대한 플라톤주의가 틀렸다고 말하는 것이 아니라 규칙에 대한 플라톤주의가 회의적 역설을 해결하는데 도움이 되지 않는다고 말하고 있는 것 같습니다. (제가 책이 없어서 앞뒤 문맥은 확인할 수 없지만 적어도 인용된 부분은 규칙에 대한 플라톤주의가 거짓이라고 주장하고 있진 않은 것 같습니다.)

설사 인용문에서 크립키가 규칙 플라톤주의가 틀렸다고 주장하고 있다고 이해될 여지가 하더라도 이 인용문이 등장하는 논의의 맥락은 의미 사실이 존재하지 않는다는 주장을 논증하기 위한 논거를 제시하는 맥락인 것처럼 보입니다. 이는 설사 크립키가 규칙 반실재론을 거부한다 하더라도 이를 의미 사실에 대한 반실재론에 "근거해서" 거부하는 것이 아님을 시사합니다. 그렇지 않다면 크립키는 순환을 범하고 있는 셈이겠죠. 왜냐하면 규칙 플라톤주의의 거짓에 근거하여 의미 사실에 대한 반실재론을 논증하고, 다시금 의미 사실에 대한 반실재론에 근거하여 규칙 플라톤주의의 거짓을 논증하는 셈일테니까요. 따라서 만약 크립키가 규칙 플라톤주의와 수학철학에서의 플라톤주의를 같은 이유에서 거부한다면 수학철학에서의 플라톤주의를 거부하는 이유는 의미 사실에 대한 반실재론일 수 없을 겁니다.

마지막으로 (a)는 특정 수학적 사실 [68+57은 125이고 5가 아니다]의 형이상학적 근거가 없다는 주장을 의도한 것입니다. 즉 @YOUN 님의 표현을 빌리자면 해당 수학적 사실이 "아무런 형이상학적 토대가 없는 상태에서 성립"하는 사실이라는 주장을 의도한 것입니다. 저는 @YOUN 님의 이전 댓글의 주장을 의미 사실에 대한 반실재론으로부터 (a)가 따라 나온다는 주장으로 이해했고 이러한 따라 나옴-관계가 성립하지 않는다는 것이 저의 주된 논점입니다. 저는 이러한 논점이 @YOUN 님의 생각과 충돌한다고 생각합니다. ((b)는 만약 '+'가 plus를 의미하는지 아니면 quus를 의미하는지 여부를 결정하는 사실이 없다면 따라 나오는 주장으로 의도한 것입니다.)

(한가지 깜박한게 있어서 덧붙이면 제가 수학철학에서의 플라톤주의를 언급한 것은 수학적 대상에 대한 가장 극단적인 종류의 실재론인 플라톤주의조차도 의미 사실에 대한 반실재론과 일관적임을 지적하기 위해서였습니다. 물론 다른 종류의 수학적 대상에 대한 실재론들도 저는 특별한 이유가 있지 않는 이상 모두 의미 사실에 대한 반실재론과 일관적이라고 생각합니다.)

4개의 좋아요
10

제 생각에는 두 분의 의견 사이의 간극이 그렇게 커 보이지는 않습니다.

  1. 크립키가 언급하는 "플라톤주의"는 수학적 실재론을 포함하고 있습니다. @YOUN 님이 인용하신 페이지 바로 이전 페이지에 다음과 같은 맥락이 나옵니다.

MathematIcal realIsts, or 'Platonists', have emphasized the non-mental nature of mathematical entities. The addition function is not in any particular mind, nor is it the common property of all minds. It has an independent, 'objective', existence. [...] (53쪽)

  1. 수학적 플라톤주의를 크립키가 언급하는 맥락은, 수학적 플라톤주의가 맞다고 하더라도, 즉 수학적 대상이 인식주체의 마음과 독립적으로 존재한다고 하더라도, 여전히 유한한 마음이 파악하는 바의 수학적 대상이 plus인지 quus인지가 결정되지 못하므로 의미회의주의가 해결되지 않는다는 것입니다. 이렇게 본다면 크립키가 수학적 실재론을 직접적으로 반박하고 있는 것은 아니라는 @mimmum 님의 지적이 타당해 보입니다.
  1. 따라서 의미 회의주의를 받아들인다고 해서 곧바로 수학적 실재론을 거부해야 하는 것은 아닙니다 (이 점은 두 분 모두 동의하고 있습니다). 그러나 다른 한편으로는, 의미 회의주의가 수학적 실재론의 매력에 큰 흠집을 내는 것도 맞다는 생각이 듭니다. 설사 수학적 대상이 실재로서 고고하게 존재한다고 하더라도, 우리가 "어떤" 수학적 대상에 인식적으로 관계하고 있는 것인지에 대한 의미 사실을 제시하지 못한다면, 수학적 실재론은 여전히 신비주의라는 비판을 피할 수 없다고 생각합니다. @YOUN 님은 아마 이러한 함축을 강조하시는 것이 아닐까 생각됩니다.

.

3개의 좋아요