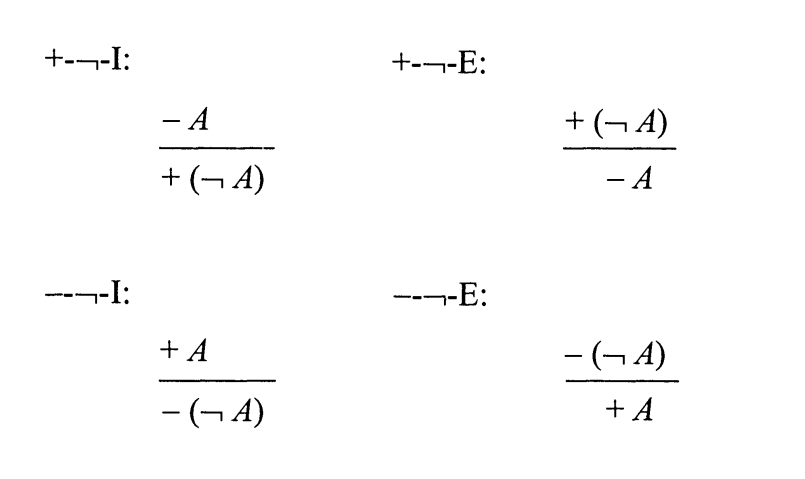조건문에 있어 도입 규칙이란 무엇인가?

논리학
1

논리학을 가르치다 보면 자연스럽게 자연 연역을 가르치게 됩니다. 공리적 증명이나 시퀀트 계산은, 강력하지만 교습자가 형식 체계에 대한 이해가 이미 있지 않으면 들이밀기 어렵죠. 진리 나무 방법은 증명이라고 하기엔 너무 덜 강력하고요. 한편, 자연 연역은 쉬우면서도 강력합니다. 공리적 증명과 마찬가지로 완전성을 겸비한 연역 체계를 구성할 수 있고, 자연어 논증과 같은 형식을 갖고 있어서 접근성도 높습니다. 논리 교육 GOAT.

한편, 자연 연역은 논리 상항들을 그 도입 규칙(I-rule)과 제거 규칙(E-rule)을 통해 정의합니다. 가령, ∧의 도입 규칙은 ‘P, Q ⇒ P ∧ Q’ 꼴로 주어지고, 제거 규칙은 ‘P ∧ Q ⇒ P’ 꼴로 주어지죠. 그런 식으로 ∨까지만 해도 잘 정의됩니다. 나아가 →와 ¬의 제거 규칙까지도요…. 문제는 마지막 두 녀석의 도입 규칙에서 등장합니다.

이 두 녀석의 도입 규칙을 위해, 전통적인 자연 연역에서는 ‘가정’(assumption)과 가정의 ‘해제’(discharge)라는 개념이 등장합니다. 그래서 대략 두 도입 규칙은 이런 식으로 소개되지요:

(1) ‘P라는 가정을 도입한 후 Q를 귀결로 얻었다고 하자. 그때 우리는 P를 해제한 뒤, P → Q를 얻는다.’
(2) ‘P라는 가정을 도입한 후 임의의 Q에 대해 Q ∧ ¬Q를 얻었다고 하자. 그때 우리는 P를 해제한 뒤, ¬P를 얻는다.’

그런데 이것들은 엄밀히 말해 ‘도입 규칙’이라고 하기 어렵습니다. 직관적으로, 도입 규칙이란 구문론적(syntactic) 절차를 제공해야 합니다. 연산자 O에 대해, 그 도입 규칙은 O를 포함 않는 문장으로부터 O를 포함하는 문장을 생성하는 절차에 관한 소개로 간주되는 것이 자연스럽단 것이죠. 그리고 이때 ‘O를 포함 않는 문장’이란, O를 갖는 언어의 대상 언어 층위 문장이어야 할 것입니다.

그런데 (1)과 (2)를 형식화하는 가장 자연스러운 꼴은 대충 다음과 같은 무엇입니다:

(1*) (P, X1, …, Xn ⇒ Q) ⇒ (X1, …, Xn ⇒ P → Q)
(2*) (P, X1, …, Xn ⇒ Q ∧ ¬Q) ⇒ (X1, …, Xn ⇒ ¬P)

띠용? 여기에서 ‘⇒’의 양항에는 대상 언어 문장이 아닌, 바로 우리가 지금 쓰고 있는 메타 언어 문장이 취해지고 있습니다.

사실, (2)의 문제는 약간의 형식적 비엄밀함을 감수한다면 다음과 같은 수정으로 개선이 가능합니다:

(2’) X → (P ∧ ¬P) ⇒ ¬X

하지만 (2’)는 여전히 ‘→’에 의존적이고, 따라서 (1)의 문제가 해결되지 않으면 ‘O가 없는 문장에서 O가 있는 문장을 만든다’라는, 도입 규칙에 대한 직관적 이해는 일관적으로 적용될 수 없게 됩니다.

이 지점에서 생각나는 해결책은 둘 정도입니다.

하나, →에 대해서는 도입 규칙을 정의하지 않는다: 이 선택지는 간편하지만, ‘논리 상항의 의미는 그 사용’이라는 비트겐슈타인적 정신을 크게 훼손합니다. 나아가, 자연 연역 체계의 완전성 또한 훼손하고 말지요.

그렇다면,

둘, →-I를 ‘조건화’라는 이름의 메타 규칙으로 밀어내고, 대신 사소한 규칙(가령, ¬P ⇒ P → Q나 Q ⇒ P → Q)을 ‘→’의 도입 규칙으로 취한다: 이 선택지는 자연 연역의 완전성을 유지하면서, →를 사용 규칙에 따라 정의할 수 있게 합니다. 대신 너무나 이상해 보이죠.

그래서 저는 둘 중 어느 것도 고를 수 없었습니다.

그렇다면 조건문에 있어 적절한, 즉, ‘도입’의 개념에 잘 부합하면서도 사소하지 않은 도입 규칙이란 무엇인가…? 여기에서 잠깐 멈춰 있습니다. 여러분께서 아시는 앞선 논의들이나 여러분의 견해가 필요합니다… 도움!

9개의 좋아요
2

negation에 관해서는 다음 논문을 인상 깊게 읽었습니다:
https://philpapers.org/rec/RUMYAN-2

image
image805×479 7.44 KB

이런 방식으로 negation을 처리하자는 제안입니다.
워낙 유명한 논문이라, 아마 알고 계실지도 모르겠지만요.

조건문은 저도 갑자기 궁금하네요.

6개의 좋아요
3

아주 흥미로운 질문이네요. 저도 고민에 동참해보고자 두 가지를 여쭙습니다.

첫째로, 지금 문제가 되는 도입규칙 두 가지는 조건증명과 간접증명에 사용되기 위해 필요한 것으로 생각됩니다. 그런데, 가령 Irving Copi의 자연연역 체계 같은 경우는 저런 규칙 없이도 완전성을 갖춘 체계인 것으로 알고 있거든요. 만약 이 문제가 Copi system에서는 문제가 되지 않는다면, 이건 특정 자연연역 체계에만 문제가 되는 것이 아닌가? 하는 의문이 들었습니다.

둘째로, 제가 기억하기로는 조건 증명법을 사용하는 것이 정당화되는 이유가 메타정리인 연역 정리(deduction theorem) 때문으로 알고 있습니다. 잘 아시겠지만, 기억나는대로 써보자면 임의 문장열 p1, p2, .., pn으로부터 q를 도출할 수 있다면 p1, p2, ..., pn-1로부터 pn->q를 도출할 수 있다는 것인데, 제가 이해하기로는 조건 증명법은 이걸 증명과정에 그대로 적용한 것 같거든요. 그럼 애초에 조건 증명법을 위한 규칙은 메타 레벨에서 주어지는 것 아닌가 하는 생각이 들었습니다!

6개의 좋아요
4

코피의 책으로는 공부해본 적이 없어 방금 잠시 살펴보았습니다. 그의 체계가 (만약 동어반복적 치환 없이도) 완전하다면, 아마도 그것은 코피의 책에서 제시되는 규칙들이 연산자의 도입/제거 규칙이 아니라 일종의 공리 스키마에 근거한 추론 규칙이기 때문일 겁니다. 또한 말씀대로, 제가 묻는 문제는 특정 체계, 특히 도입/제거 규칙에 근간을 둔 자연 연역에서만 발생합니다. (당연한 소리이긴 합니다 ㅋㅋ;;)

그런데 제게는 이게 단지 연역 체계뿐 아니라 논리 연산자들의 성격 규정에 있어 제기되는 꽤나 근본적인 문제로 보입니다. 언급한 것처럼, 만약 우리가 논리 연산자의 의미를 그 추론 규칙으로 본다면, 어떤 문장열 스키마로부터 어떤 문장 스키마가 연역된다는 꼴로 한정된 도입/제거 규칙만으로 모든 연산자가 정의되어야 할 것 같습니다. 그런데 그렇지가 못하다는 것이죠.

웃기게도, 논리 연산자의 의미를 그 추론 규칙에서 보자고 한 해리스(Harris 1982)조차 조건문의 경우는 MP와 Deduction theorem을 통해 캐릭터라이징합니다. 왜 조건문에 대해서만 이런 특이한 상황이 발생하는지… 앞선 연구가 많을 것 같은데 알고 계신 회원이 있다면 좋겠네요.

ps: 이런 맥락에서 제가 얼마 전에 해리스의 풀네임을 애타게 찾은 것이랍니다:wink:

7개의 좋아요
5

사실 저는 이게 왜 문제가 되는지 잘 모르겠어요. 그래서 다음 인용문에서 언급된 '자연스러움'도 이해가 잘 가지 않네요.

나중에 제 답변을 추가로 달게요.

2개의 좋아요
6

마틴뢰프에 따르면, 추론의 대상은 명제가 아닌 판단(judgment)입니다: On the meanings of the logical constants and the justifications of the logical laws

마틴뢰프는 직관주의자이고, 마틴뢰프가 명제와 판단의 구분을 적극적으로 도입한 이유가 그의 직관주의적 타입이론과 관계가 있긴 하지만, 명제와 판단의 구분이 필요하다는 주장은 직관주의적 입장과 별개로 수용될 수 있습니다: 직관주의적 유형론에서의 진리개념

명제와 판단의 구분을 받아들인다고 할 때, 연언의 도입 소거 규칙은 다음과 같이 형식화 합니다.

ϕ true  ψ true
-------------- ∧I
  ϕ ∧ ψ true

ϕ ∧ ψ true
---------- ∧E₁
  ϕ true

ϕ ∧ ψ true
---------- ∧E₂
  ψ true

여기서 ϕ true는 ϕ가 참임을 주장하는 판단입니다 (진리 판단이라고 부르겠습니다). 추론의 전제와 결론에는 명제나 대상언어의 문장이 아닌 판단이 위치합니다.

그런데 판단은 메타적인 서술입니다. 예를 들어 ϕ true, (ϕ true) ∧ (ψ true), (ϕ true) true 등은 올바른 대상 언어의 문장으로 간주되지 않습니다. 만약 아래에서 인용한 부분이 "추론규칙의 전제들과 결론은 대상언어의 문장이다"를 함의하는 것을 의도로 쓰셨다면, 저는 그에 동의하지 않습니다.

그런데 이것들은 엄밀히 말해 ‘도입 규칙’이라고 하기 어렵습니다. 직관적으로, 도입 규칙이란 구문론적(syntactic) 절차를 제공해야 합니다. 연산자 O에 대해, 그 도입 규칙은 O를 포함 않는 문장으로부터 O를 포함하는 문장을 생성하는 절차에 관한 소개로 간주되는 것이 자연스럽단 것이죠. 그리고 이때 ‘O를 포함 않는 문장’이란, O를 갖는 언어의 대상 언어 층위 문장이어야 할 것입니다.

제 입장에 따라 도입 규칙에 대한 설명을 수정하면 다음과 같습니다.

논리 연결사 X의 도입 규칙은, 결론이 X로 구성된 문장에 대한 진리 판단이고, 전제가 이 문장의 X를 포함하지 않는 구성 문장들에 대한 진리 판단인 규칙이다.

구체적으로 함언의 도입규칙이 어떻게 생겼는지 보자면, 마틴뢰프는 가언 판단 (hypothetical judgment) 이라는 개념을 도입해 다음과 같이 표기합니다.

ϕ true | ψ true
--------------- →I
  ϕ → ψ true

ϕ true | ψ true는 ϕ true를 가정했을 때 ψ true를 도출할 수 있음을 뜻하는 가언 판단입니다. 형식적으로 보면 겐첸의 것과 특별히 다르진 않습니다.

혹은 제시하신 (1*)의 규칙과 비슷하게, 아래의 형태로도 많이 씁니다.

Γ, ϕ true ⊢ ψ true
------------------ →I
  Γ ⊢ ϕ → ψ true

여기서 Γ는 ϕ₁ true, ⋯, ϕₙ true를 줄여 쓴 것입니다.

명제와 판단의 구분을 전제로 하는 Frank Pfenning 교수님의 Constructive Logic 강의 자료가 공개되어있는데, 개인적으로 굉장히 추천합니다.

가언 판단에 대한 보다 형식적인 설명은 Robert Harper 교수님의 Practical Foundations for Programming Languages 1장에서 다룹니다.

3개의 좋아요
7

마틴-뢰프의 도식에서도 무언가 꼬롬한 점이 여전히 남는 듯합니다. 다른 도식들이 단적인 판단들로부터 단적인 판단을 내놓는다면, 조건 도입의 경우에는 ‘가언 판단’이라는 독특한 종류의 판단으로부터 단적인 판단을 이끌어냅니다. ‘도입 규칙’이라고 일관되게 말하기에는 가언 판단 혼자 튀는 모양새를 갖는 것이죠. 왜 다른가? 차라리 조건문에 대한 규칙을 별개의 범주에 두고, ‘조건 도입’ 내지는 implication 도입은 다른 형태의 도식을 가져야 하는 것인가? 이게 제 질문이기는 합니다.

2개의 좋아요
8

덧,
그리고 선생님의 정식화인

에 마틴-뢰프식 규칙 정의는 사실 잘 부합하지 않습니다. 한편으로는 P true가 ‘결론’으로 P를 갖는다고 보기 어렵고, 다른 한편으로는 ‘가언 판단’이 ‘문장에 대한 진리 판단’이라고 보기 어렵기 때문입니다.

2개의 좋아요
9

맞습니다, 해당 설명은 가언 판단이 필요없는 연결사 정도만 완전히 들어맞고 가언 판단이 필요한 경우에 대해서는 부정확합니다. 해당 설명은 도입 규칙을 완전히 해설하기 위함이 아니라 추론이 문장이 아닌 판단에 대한 것임을 강조하기 위함이므로 간추려 설명했습니다.

한편으로는 P true가 ‘결론’으로 P를 갖는다고 보기 어렵고

이 부분은 어떤 말씀인지 이해 못했습니다. '결론'은 판단이 되어야 하므로 P true 꼴의 메타언어 표현이 와야 합니다.

2개의 좋아요
10

추론규칙 마다 다른 종류의 판단이 사용 되는 것이 불편하다면, 마틴뢰프의 철학에선 다소 멀어지게 되지만 진리 판단에 맥락 Γ를 추가한 Γ ⊢ φ를 유일한 판단으로 도입하는 것도 좋은 방법이라고 생각합니다. (판단의 문법적인 형태만 놓고 보면 직관주의 시퀀트 계산과 같습니다)

이런 형태의 판단을 사용하는 자연연역의 몇가지 규칙은 다음과 같습니다.

Γ ⊢ φ  Γ ⊢ ψ
------------- ∧I
Γ ⊢ φ ∧ ψ


Γ, φ ⊢ ψ
---------- →I
Γ ⊢ φ → ψ

사실 이 형식화는 가언 판단에 대한 철학적 논의를 피할 수 있기 때문에 좀 더 맘 놓고 쓸 수 있는것 같습니다. 현대 수리논리 분야에서도 가언판단 보다는 이런 방식을 더 흔하게 사용하는것 같구요. (가령 Categorical Logic and Type Theory의 FOL 형식화)

덧붙여서, 함언 도입 규칙뿐만 아니라 선언 소거 규칙도 가언 판단이나 맥락등을 필요로 합니다.

Γ ⊢ φ ∨ ψ  Γ, φ ⊢ χ  Γ, ψ ⊢ χ
------------------------------
Γ ⊢ χ
4개의 좋아요
11

아! 이해됐습니다. 감사합니다. 다만 이 경우 귀납 기초가 존재하지 않아 증명을 정의할 수 없는 게 아닌가 싶긴 한데요, 생각을 해보아야겠습니다. 관련해 아시는 게 있다면 알려주시면 감사하겠습니다.

1개의 좋아요
12

귀납 기초에 대해서는, 다음의 가정 규칙을 추가해야 합니다

φ ∈ Γ
------ hyp
Γ ⊢ φ
1개의 좋아요
13

흥미롭네요. 개인적으로는 동어반복을 베이스 스키마로 두고 논증 가지들의 전제의 합집합으로부터 도입되는 명제가 함축되는 형태로 결론을 쓰는 게 더 아름다워보이긴 합니다.

말하자면 마틴-뢰프식 방법은 언어를 두 층위가 아니라 세 층위로 둠으로써 도입 및 제거 규칙을 통해 연산자를 정의하는 것이군요. 흥미롭습니다. 공부가 되었네요. 감사합니다.

(생각해보니 이렇게 하면 구조상 lemmon style과 동등하네요.)

4개의 좋아요
14

@damhiya 님이 이미 다 잘 설명하셔서 저는 하나만 덧붙일까 해요.

마리오 카네이로(Mario Carneiro) 박사님이 위와 같은 자연 연역 규칙들을 힐베르트식 체계에 맞게 고치는 방법을 예전에 제시하셨어요.

⊢ Γ → φ  ⊢ Γ → ψ
---------------- ∧I
⊢ Γ → φ ∧ ψ

⊢ Γ ∧ φ → ψ
------------- →I
⊢ Γ → (φ → ψ)

여기서 Γ는 더 이상 맥락[context]이 아니고, 그저 φ, ψ와 같은 문장(명제, 대상 언어의 식)일 뿐이에요. 맥락처럼 여길 수는 있겠지만요.

위의 수정된 조건문 도입 규칙은 @car_nap 님이 말씀하신 요건을 충족하지 않죠. 그래서 참고만 하시면 좋을 듯해요.

원래의 자연 연역 규칙과 그 번역을 비교한 표는 다음 링크의 웹 문서에서 확인하실 수 있어요.

https://us.metamath.org/mpeuni/natded.html

다음은 마리오 카네이로 박사님의 2014년 '메타매스 증명 언어에서의 자연 연역' 발표 자료입니다.

1개의 좋아요