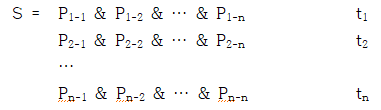제7장 개체의 시간적 지속
실체의 지속이라는 문제는 시간 및 변화의 문제와 결부되어 있다. 통상적으로 시간은 하나의 직선으로 표상되며, 변화란 그 중 한 시점에서 실체 A가 속성 P를 갖지 않고 다른 점에서는 P를 갖는 일로 생각되었다. 또 지속은 서로 다른 시점 속에서 A가 동일하다는 뜻으로 생각되었다. 그러나 라이프니츠는 시간, 변화, 지속을 완전히 다르게 생각한다.
1. 시간
앞 장에서 살펴봤듯, 라이프니츠는 시간을 사물의 주기적 운동 및 이 사물이 다른 사물들과 맺는 관계로 환원한다. 사물들의 관계로부터 우리는 시간이라는 관념을 형성한다. 그런데 획득된 시간 관념은 현실세계뿐만이 아니라 가능세계들에도 일반화되어 적용된다.
라이프니츠는 이러한 일반화된 시간 개념을 다음처럼 정의한다. “시간이란 서로 모순을 일으키는 단항 용어(terme)들 사이의 존재(d’exister)의 질서/순서이다.”(Recherches, 109, 박제철, 2013, 155에서 재인용) 라이프니츠에서 ‘용어’(terme)가 관념 혹은 개념을 뜻한다는 점을 고려할 때, 이 정의에 대한 두 가지 해석이 가능하다. 그 중 하나는 시간이 존재의 순서라는 점에 방점을 두고 해석하는 길이다. 그에 따르면 시간은 실재하는 사물들 사이의 관계를 뜻하기 때문에 현실세계에만 적용될 뿐 한낱 관념에 불과한 가능세계에는 적용되지 않는다. 그러나 라이프니츠는 “상상적으로 가능한 것”(le possible imaginaire) 즉 가능세계의 사물들 역시 현실적인 것과 마찬가지로 시간적 및 공간적 질서를 따른다고 말한다. 그러므로 시간이 존재의 순서라는 점을 강조하는 해석은 라이프니츠 자신의 주장과 충돌한다. 혹자는 현실적인 사물들이 현실적으로 실재하는 것과 마찬가지로 가능적인 사물들 역시 가능적으로 실재한다고 말할 수 있겠으나, 라이프니츠에서 가능적인 사물들은 신의 정신 안에 존재하는 관념인 까닭에 이러한 대안 역시 불가능하다.
그러므로 우리에게는 시간의 관념성을 강조하는 다른 쪽 길만이 남는다. 라이프니츠의 존재론이 모나드와 그 속성들로 이루어져 있듯 라이프니츠의 관념 이론 역시 완전 개체 개념과 그 요소 개념들로 이루어진다는 점을 상기하자. 이제 라이프니츠의 시간 및 변화, 지속 개념은 동시적 집합이라는 개념을 통해 설명될 수 있다. 동시적 집합이란 “완전 개체 개념 […] 내의 서로 동시적인 요소 개념들로 이루어진 집합”(박제철, 2013, 160)을 말한다. 제4장에서 제시되었던 완전 개체 개념에 관한 정식화를 상기하자.
여기서 각 순서 tn에서 존재하는 속성들의 집합 {Pn-1, Pn-2, … Pn-n}이 동시적 집합이며, 이 동시적 집합들이 순서지어진 계열 S가 바로 완전 개체 개념이다. 여기서 서로 다른 동시적 집합은 “서로 모순을 일으키는 단항 용어들”을 갖는다. 예컨대 한 동시적 집합은 정직함을 원소로 갖는 반면 다른 동시적 집합은 부정직함을 원소로 갖는다. 시간이란 이처럼 모순적인 용어들을 내포하는 동시적 집합들의 질서를 일컫는다. 이들의 순서는 앞 장에서 보았듯 어떤 집합이 더 단순하고 더 복잡한지, 어떤 집합이 더 불완전하고 더 완전한지 등에 따라 결정된다.
그런데 복잡성과 완전성의 계열이 어떻게 단순한 논리적 계열과 달리 시간적 계열일 수 있는가? 시간이 변화를 함축한다는 점에서 그렇다. 동시적 집합들의 계열은 변화를 설명함으로써 다른 논리적 계열들과 변별될 수 있다.
3. 변화
라이프니츠는 변화를 다음처럼 정의한다. “만약 A가 B이고, 바로 그 A에 대해, A는 non-B이면, 우리는 A 안에서 변화가 일어났다고 말한다. […] 만약 티티우스가 정직하지만, 그 다음에(par la suite) 그 티티우스가 부정직하다면, 우리는 티티우스 안에서 변화가 일어났다고 말[한다.]”(Recherches, 393, 박제철, 2013, 162에서 재인용)
4. 가능한 해석들
이 구절은 일견 다음처럼 해석되는 듯 보인다.
x는 변화한다 ↔ x는 P이면서 P가 아니다.
그러나 이는 잘못이다. 라이프니츠가 보기에 모순적인 것은 불가능한 것인 반면, 실체들은 가능할 뿐만 아니라 실재한다. 그러므로 이러한 해석은 라이프니츠의 주장과 어긋난다. 우리는 정합적인 해석을 위해 “그 다음에(par la suite)”라는 단어에 주목함으로써 매개변항 t를 추가해야 한다.
x는 변화한다 ↔ x는 tn에서 P이면서 tn+1에서 P가 아니다.
이때 이전의 해석에서 발생하는 모순을 해소하는 매개변항 tn과 tn+1은 주어 x를 변양한다(modify). 시간 매개변항이 주어를 변양한다는 것은, 전자가 후자의 “한 측면에 관해 정보를 준다”(박제철, 2013, 163)는 뜻이다. 주의할 점은 여기서 변양되는 주어의 측면이 시간축의 한 시점이 아니라 동시적 집합이라는 점이다.
이제 시간적 변화는 동시적 집합들의 순서로 분석될 수 있다. 즉
x는 변화한다 ↔ x는 tn에서 P이면서 tn+1에서 P가 아니다.
는 x를 구성하는 동시적 집합 x-Cn과 x-Cn+1에 대해
x는 변화한다 ↔ x-Cn은 P를 원소로 가지며 x-Cn+1은 P를 원소로 갖지 않는다.
를 뜻한다.
5. 시간 t가 술어 개념을 꾸밀 가능성은 없는가?
앞 절에서 t는 주어를 변양하는 매개변항으로 이해되어 x-Cn과 x-Cn+1로 환원되었다. 한데 t가 술어에 귀속되는 해석 역시 논리적으로는 가능할 터이다.
x는 변화한다 ↔ x는 P-tn이면서 P-tn+1이 아니다.
그러나 이는 앞서의 정의에 적합한 정식화라고 할 수 없다. 왜냐하면 시간에 대한 라이프니츠적 정의는 “서로 모순을 일으키는 단항 용어들”을 포함하기 때문이다. 반면 P-tn과 P-tn+1은 서로 모순을 일으키지 않는다.
6. 지속
라이프니츠는 실체가 시간 속에서 동일한 것으로 지속한다고 믿는다. 그에 의하면 내가 지속하는 선험적(a priori) 이유는 예전의 속성과 지금의 속성이 하나의 동일한 주어에 귀속된다는 것이다. 그런데 이는 곧 “술어 개념이 어떤 방식으로든 주어 개념 안에 포함되어 있다는 말”(Le Roy, 109, 박제철, 2013, 168)이다. 즉 실체의 지속은 주어 개념이 여러 속성을 묶는다는, 혹은 포함한다는 데에서 성립한다. 실체의 지속은 개념, 관념과 관련하여 설명되고 있다. 이제 완전 개체 개념이 동시적 집합들의 계열로 정의된다는 점을 상기하자면, 실체 S가 tn에서 tn+1까지 지속하는 선험적 이유는 그 개념 ‘S’가 동시적 집합 S-Cn과 S-Cn+1을 묶기 때문, 혹은 그 안에 포함하기 때문이다.
7. 선험적 이유는 왜 필요한가?
실체의 지속에 대해 라이프니츠가 이러한 이유를 제시하는 이유가 무엇인가? 라이프니츠 자신은 이 이상 설명을 제공하지 않지만, 우리는 라이프니츠가 실체의 단순한 동일성(identity simpliciter)을 거부하기 때문이라고 추정해볼 수 있다. 먼저 동일성 개념은 단순한 동일성, 수적 동일성(numerical identity), 동시적 동일성(synchronic identity), 비동시적 동일성(diachronic identity)으로 나뉜다. 예컨대 “A는 A와 동일하다”는 단순한 동일성, “지금의 A는 지금의 A와 동일하다”는 동시적 동일성, “어제의 A와 오늘의 A는 동일하다”는 비동시적 동일성을 나타낸다. 그런데 라이프니츠는 다음처럼 묻는다. “왜 내가 지속한다고 말할 수 있는가? 왜 파리에 있었던 내가 지금은 독일에 있다고 말할 수 있는가? 아무런 이유가 없다면, 이 둘은 서로 다르다고 말하는 것이 옳아 보이기에 말이다.”(Le Roy, 109, 박제철, 2013, 168) 라이프니츠에 의하면, 예전에 파리에 있었던 나와 지금 독일에 있는 나는, 양자의 동일성을 뒷받침할 이유가 딱히 없다면 다르다고 보아야 한다. 만일 라이프니츠가 실체의 단순한 동일성을 인정했다면, 양자의 동일성을 주장하기 위해 추가적인 근거를 제시하는 일이 필요하다고 생각할 이유가 없었을 것이다. 그러므로 라이프니츠는 단순한 동일성을 인정하지 않는다.
그러나 그는 양자가 동일하다고 볼 근거가 있다고 생각하며, 따라서 비동시적 동일성은 인정한다. 그리고 실체가 비동시적으로 지속한다고 볼 이유는 앞서 설명되었듯 실체의 완전 개체 개념이 상이한 동시적 집합들을 묶고 있기 때문이다.
8. 지속: ‘묶음’ 관계
결국 실체의 지속을 보장하는 것은 속성 다발들의 묶임 관계이다. 이 묶임 관계는 어떻게 지속을 보장하는가? 그 이유는 라이프니츠의 지속 이론을 일종의 펼침 지속 이론(perdurantism)으로 해석함으로써 제시될 수 있다. 실체가 시간축을 이동하면서 지속한다는 견딤 지속 이론(endurantism)과 달리, 펼침 지속 이론에 의하면 실체는 시간적으로 연장되어 있기 때문에 지속한다. 실체는 서로 다른 시점들 속에서 상이한 부분들을 지니며, 실체가 지속한다는 것은 이 부분들이 서로 연결되어 있다는 뜻이다. 지속하는 실체란 상이한 시간적 부분들에 의해 이루어지는 전체이다.
라이프니츠의 실체 개념 역시 상이한 동시적 집합에 의해 이루어진 계열이라는 점을 상기한다면, 라이프니츠의 실체 이론이 펼침 지속 이론의 하나라는 점이 이해 가능하다. 실체가 지속한다는 것은, 실체가 서로 다른 동시적 집합들에 의해 구성되어 있다는 뜻에 다름 아니다. 이 묶음 관계가 실체의 비동시적 동일성에 대한 선험적 이유에 다름 아니다.
9. 결론
라이프니츠에 의하면 시간은 동시적 집합들의 계열로 환원되며, 이 동시적 집합들 사이의 상이성이 실체의 변화를, 이들 사이에 성립하는 묶음 관계가 실체의 지속을 가능케 한다.