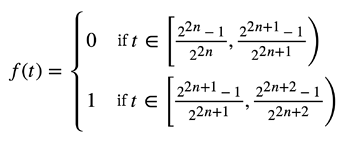(해당 에세이는 2022년 가을학기 이승종 교수님의 수업 과제로 제출한 레포트입니다. 오늘 성적 입력이 완료되었길래 정보 공유 차원에서 올립니다.)
서론
⟪비트겐슈타인 새로 읽기⟫(이승종 2022, 이하 NRW)는 사람이 언어와 수학을 사용하는 현상을 “사람의 얼굴을 한 자연주의”의 관점에서 해명하려는 시도이다. 이승종 교수에 따르면 PI, §415와 PPF, §365 등의 구절은 비트겐슈타인이 확실성의 지평을 자연사의 관점에서 해명하고 있으나, 그의 관심사는 자연사 전체가 아닌 “사람의 자연사”에 국한되어 있음을 보여준다(NRW, p. 109-113). 비트겐슈타인의 철학적 작업은 “자연사 그 자체가 아니라 자연사의 지평에서 펼쳐지는 인간 현상을 관찰하고 기술”함으로써 “우리가 자연에 터를 둔 사람의 관점에서 세상을 살고 세상을 본다는 지극히 자명한 사실을 우리에게 환기”(NRW, p. 110)하기 위함이라는 것이 이승종 교수의 해석이다.
1부에서 “사람의 얼굴을 한 자연주의”의 얼개를 제시한 이승종 교수는 2부에서 이를 수학에 접목한다. 비트겐슈타인의 수학철학을 토대로 이승종 교수는 플라톤주의와 규약주의라는 수학철학의 양극단에 위치한 두 진영을 모두 공격한 후, 대안으로 수학의 필연성과 강제력을 삶의 형식과 자연사의 관점에서 해명한다. 수학의 필연성의 기원은 다름아닌 “판단에서의 일치, 삶의 형식에서의 일치, [그리고] 자연의 제일성”(NRW, p. 219)이다. 그러나 일치는 충분조건이 아니기에 우리는 주어진 삶의 형식과 자연사를 배경으로 상이한 수학 체계를 상상할 수 있다. 그러한 수학 체계들은 마치 “캡슐”과도 같은 내적 자율성을 가지며, 캡슐 내부의 “필연적 강제력”(NRW, p. 224)과 캡슐 외부의 자연사적 필연성이 수학적 필연성의 제반을 형성한다. 이렇게 해명된 수학적 필연성은 “자연사적 사실과 삶의 형식의 국소성, 상대성, 변동가능성에 접맥”(NRW, p. 225)되어 있기에, 이로써 “플라톤주의와 규약주의의 양극단을 피해 수학적 필연성을 보존하면서도 변화의 역동성을 적절히 해명”할 수 있다고 이승종 교수는 주장한다.
본 소론에서 필자는 이승종 교수가 제시한 수학의 자연주의적 해석에 보론과 비판을 제시할 것이다. 구체적으로, 논리학의 자연화와 모순론에 관하여 보론을, 수학의 자연화에 관하여 비판을 제시할 것이다.
1. 논리학의 자연화에 관한 보론
이승종 교수는 다음과 같이 주장한다.
물리적, 생물학적 환경 등 사람의 자연사의 사실들은 사람의 인류학적 삶의 형식과 함께 그의 생각과 추론의 패턴을 조건 짓는다. 그리고 이 패턴은 논리학과 수학의 기본 법칙들로 고착된다. (NRW, p. 215, 필자에 의한 강조)
이승종 교수는 ‘생각과 추론의 패턴’의 사례로 무엇이 있는지 구체적으로 밝히지 않는다. 필자는 Garver(1996)에서 제시된 양립 불가능성 논증을 강화해 패턴 고착화의 두 가지 사례를 직접 제시하고자 한다.
소쉬르에 따르면 모든 의미 체계는 부정의 개념을 기반으로 형성된다. 즉, A가 유의미한 개념이라는 것은 곧 A를 발화할 수 있는 상황과 없는 상황이 나누어져 있다는 것이다. ‘새파랗다’를 발화할 수 있는 상황에서 ‘파랗다’를 발화하는 것은 괜찮지만, ‘붉다’를 발화할 수 있는 상황에서 ‘파랗다’를 발화하는 것은 허용되지 않는다. 이러한 허용과 불허의 관계가 ‘파랗다’의 의미를 형성한다.
이것은 다음과 같이 정식화할 수 있다. 어떤 언어게임 G가 있다고 하자. G에서 유의미한 상황의 집합을 Sa(G)라고 하고, G에서 사용되는 발화의 집합을 Pr(G)라고 하자. G를 이해하기 위한 필요조건은 다음의 집합 Sem(G)를 체득하는 것이다.
Sem(G) = { {P, Q} ⊂ Pr(G) | ¬∃x ∈ Sa(G) [⬦P(x) ∧ ⬦Q(x) ] }
여기에서 ⬦는 가능성을 의미하며, P(x)는 ‘상황 x에서 P를 발화한다’를 의미한다. 따라서 {P, Q} ∈ Sem(G)는 ‘P의 발화와 Q의 발화가 모두 가능한 상황은 없다’를 의미한다. 구체적인 사례로서, 다음과 같이 B, BB, R을 정의하자.
B: “파랗다”
BB: “새파랗다”
R: “붉다”
Pr(G) = {B, BB, R}, Sa(G) = {“사과를 가리킴”, “하늘을 가리킴”}이라면 Sem(G)는 다음과 같다.
{ {B, R}, {BB, R} }
분명히 해야 하는 사실이 세 가지 있다. 첫째, ⬦의 규범성은 자연주의적이며, 형이상학적이지 않다. ⬦P(x)의 의미는 단순히 상황 x에서 P를 발화하는 경우가 있었다는 의미이고, ¬⬦P(x)의 의미는 단순히 상황 x에서 P를 발화하는 경우가 없었다는 의미이다. 따라서 {P, Q} ∈ Sem(G)의 의미는 P와 Q를 모두 발화하는 경우는 없었다는 의미이다. 이것은 G가 오랜 과거부터 지속되어 왔다는 자연사적 사실에 기반한 기술적 진술이며, 양상 논리의 형이상학적 문제는 이 논의와 무관하다. 후술하겠지만, 필자는 오히려 ⬦의 의미를 상술한 바와 같이 재해석하였을 때 규범성의 진상이 드러난다고 생각한다.
둘째, Sem(G)를 체득하는 것은 G를 숙지하기 위한 충분조건이 아니다. Sem(G)만 체득한 화자는 ‘새파랗다’가 ‘파랗다’를 함의하지만, 그 역은 성립하지 않는다는 사실을 모르기 때문이다. 그러나 분명한 것은, G가 언어게임이라면 G는 Sem(G)를 필요로 한다는 사실이다. Sem(G)는 G에서 무절제한 발화 — ‘붉다’고 말할 상황에서 ‘파랗다’고 말하는 따위의 행위 — 가 일어나지 않도록 제약하는 최소한의 규정이기에 Sem(G)를 결여한 발화 행위는 언어게임이 아닌, 백색 소음에 지나지 않는다.
셋째, Sem(G)를 체득하는 것은 하나의 실천(PI, §202)이다. Sem(G)는 G로부터 분리되어 있지 않다. 다시 말해, Pr(G)의 수많은 멱집합 중 어느 것이 올바른 Sem(G)인지 결정하는 문제는 일어나지 않는다. NRW의 8장에서는 “사람들이 규칙(Sem(G))에 대해서 일치를 본다 함은 규칙 따르기(G)에 있어서 일치를 본다는 것에 본질적으로 의존해 있다”(NRW, p. 277, 필자에 의한 괄호)라는 지적을 비롯하여 이 논의가 상세히 이루어져 있다.
사람이 언어를 사용한다는 것은 자연사적 사실로 주어져 있다. 다시 말해, 모든 사람은 어린 시절 자연스럽게 언어게임에 참여하여 언어의 사용을 익힌다. 그리고 언어를 익히는 과정은 Sem(G)를 체득하는 과정을 내포하며, 이 과정은 ¬(⬦P ∧ ⬦Q)라는 가장 기본적인 “생각과 추론의 패턴”을 정착시킨다. 이제 이 패턴이 어떻게 “논리학의 기본 법칙들로 고착”되는지 알아보자.
먼저 ¬(⬦P ∧ ⬦Q)의 패턴은 술어 논리의 모든 명제를 구축하기에 충분하다. Φ(P, Q)를 ¬(⬦P ∧ ⬦Q)로 정의하고, ⬦P와 ⬦Q를 각각 A와 B로 두자. 그렇다면,
Φ(P, P) ≡ ¬A
Φ(Φ(P, P), Φ(Q, Q)) ≡ A ∨ B
Φ(Φ(P, Q), Φ(P, Q)) ≡ A ∧ B
이다. 따라서 상술한 생각과 추론의 기본적인 패턴은 논리 언어를 이해할 수 있는 충분조건을 마련한다(Garver 1996).
또다른 예시로 양상 논리를 살펴보자. 필연성을 의미하는 기호 □를 도입하자. □¬P(x)는 ‘상황 x에서 P를 발화하지 않아야 한다’라는 의미이다. 다시 한번, 여기에서 규범성은 형이상학적인 의미가 아닌 자연주의적 의미이다. □¬P(x)는 ‘상황 x에서 P를 발화하는 것은 언어게임의 참가자들을 당황스럽게 만든다’, 또는 이와 비슷한 의미로 해석될 것이다.
이해를 돕기 위한 가상의 시나리오로, G의 규칙을 모르는 철수가 G에 참여하기 위해 G의 참가자들이 나누는 발화를 지켜보고 있다고 하자. 오랜 관찰을 통해 철수는 P를 발화하기도 하고 Q를 발화하기도 하는 상황이 없다고 추측한다. 그럼에도 철수가 ⬦P(y)인 상황 y에서 Q를 발화하면 어떤 일이 일어날까? 철수는 G의 참가자들이 당황스러워하는 것을 본다. 즉, 철수는 ¬⬦Q(y)로부터 □¬Q(y)를 본다. 이것은 다음의 양상 논리 규칙으로 고착된다.
¬⬦ ≡ □¬
즉, 가능성과 필연성이라는 두 양상 개념의 원천은, ‘언어게임에서 무의미한(가능하지 않은) 발화 행위를 하는 것은 언어게임 참가자들의 배척을 유발한다(해서는 안 된다)’라는 자연사적 사실이다. 이러한 자연사적 사실이 성립하는 근거는 “[의견에서의 일치 이전에] 무엇이 의미 있다, 무엇이 무의미하다 등과 같은 판단의 테두리에서의 일치가 먼저 전제되어야 한다”(NRW, p. 66)고 지적한 이승종 교수의 단상과 유관하다.
2. 모순론에 관한 보론
본 소론에서 필자는 톰슨의 역설을 통해 비트겐슈타인 모순론의 적용 사례를 제시하고자 한다. 톰슨의 역설은 다음과 같다. 전원이 꺼져 있는 램프가 있다. 1/2분이 지나면 램프의 전원을 켠다. 1/4분이 더 지나면 램프의 전원을 다시 끈다. 1/8분이 더 지나면 다시 켜고, 이런 작업을 반복한다. 즉, t분 후 램프의 상태는 다음과 같다.
그렇다면 1분이 흘렀을 때 램프의 전원은 켜져 있는가, 꺼져 있는가? 이 역설을 제시한 톰슨은 램프가 켜져 있을 수도, 꺼져 있을 수도 없다고 주장했다. 켜져 있을 수 없는 이유는 램프를 켜는 단계 이후 램프를 끄는 단계가 항상 있기 때문이고, 램프가 꺼져 있을 수 없는 이유 역시 마찬가지이다(Thomson 1954).
이것은 분명 모순이다. 그러나 비트겐슈타인의 모순론에 따르면 이것은 전혀 심각한 문제가 아니다. 비트겐슈타인이라면 이렇게 답할 것이다. 함수 f에 부합하는¹ 램프가 생활 세계에 존재하지 않는다면 톰슨의 역설은 우리와 무관하다. 그러나 함수 f에 부합하는 램프가 생활 세계에 존재한다면, 톰슨의 역설이 완전히 기술하지 못한, 혹은 부적절하게 기술한 램프의 ‘맥락’이 역설을 자연스럽게 해소할 것이다.
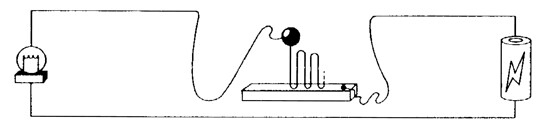
후자의 경우에 관한 실례로서 Earman과 Norton이 고안한 아래의 램프를 보자(Earman & Norton, 1996). 구슬이 금속판에 부딪히면 회로가 연결되어 램프가 켜지고, 구슬은 이전 단계보다 조금 낮은 높이로 튕겨 오른다. 금속판의 탄성 계수를 적절하게 조절함으로써 아래 램프가 함수 f에 부합하도록 만들 수 있다. 그러나 1분 후 램프의 상태는 명확하다. 램프는 켜져 있다.
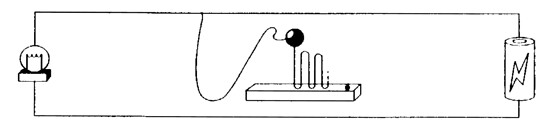
반대의 사례도 가능하다. 아래 램프의 경우, 구슬이 금속판에 부딪히면 회로가 접지되어 램프가 꺼진다. 이 역시 f에 부합하는 램프이지만, 1분 후 램프는 꺼져 있다.
이렇듯 생활 세계와 접맥되는 순간 톰슨의 역설은 자연스레 해소된다. 톰슨의 역설이 역설처럼 보이는 이유는 생활 세계와 유리된 공간에서 오로지 추상적인 논증과 논리 규칙만을 통해 역설을 해결하려 시도했기 때문이다. 하지만 문제는 유한 구간에서 발산하는 수열을 허용하는 해석학의 이론에 있는 것이 아니라, 그 이론을 어떻게 회로에 적용할지가 부적절하게, 그리고 불충분하게 설정된 데 있다. 즉, “모순된 계산법…이 문제가 된 것이 아니라, 계산법…의 선택이 잘못된 것이다(NRW, p. 318)”.
이것은 모순을 대하는 자연스러운 태도이자, 비트겐슈타인이 강조하는 태도이다. 톰슨의 역설과 폭발 원리를 근거로 유니콘이 존재한다고 주장하는 사람은 아무도 없다. 대신 톰슨의 역설을 마주한 사람의 “자연스러운 태도는 그로부터 무언가를 이끌어 내는 것이 아니라, 일종의 막다른 골목으로 여겨 그로부터는 아무것도 할 수 없다고 여기는 것이다(NRW, p. 318)”. 막다른 골목에서 벗어났을 때 우리는 톰슨 램프가 생활 세계와 접맥됨으로써 해소되는 문제임을 이해할 수 있다.
필자의 요지를 명확하게 하기 위해서 퍼트넘이 제시한 사례를 거론하겠다(Putnam 1967). 퍼트넘은 수학의 명제와 생활 세계의 사태가 다리 원리(Bridge Principle)들에 의해 매개된다고 주장한다. 예를 들어 우리에게 다음이 주어져 있다고 하자.
(1) 정확히 한 개의 사과가 있다. ( ∃x(Ax ∧ ∀y(Ay → x = y)) )
(2) 정확히 한 개의 바나나가 있다. ( ∃x(Bx ∧ ∀y(By → x = y)) )
(3) 사과이면서 바나나인 것은 없다. ( ¬∃x(Ax ∧ Bx) )
이로부터 사과이거나 바나나인 것의 개수를 추론하기 위해서 우리는 논리학의 추론 규칙을 따를 수 있다. 그러나 그 과정은 매우 복잡하다. 대신 우리는 다리 원리를 통해 훨씬 편하게 추론을 진행할 수 있다. 먼저 위의 세 사태를 아래의 세 수학적 명제로 변환하는 다리 원리를 도입한다.
(a) #x(Ax) = 1
(b) #x(Bx) = 1
(c) #x(Ax ∧ Bx) = 0
다리 원리를 건넘으로써 이제 우리는 수학의 영역으로 진입했다. 수학의 영역에서 우리는 명제 (AR)과 추론 규칙 (CA)을 사용할 수 있다.
(AR) 1 + 1 = 2
(CA) #x(Fx) = m, #x(Gx) = n, #x(Fx ∧ Gx) = 0 ⊢ #x(Fx ∨ Gx) = m + n
(a) ~ (c)에 (AR)과 함께 (CA)를 적용하면 다음을 얻는다.
(d) #x(Ax ∨ Bx) = 2
이제 다시 다리 원리를 건너 생활 세계의 영역으로 돌아오면 다음을 얻는다.
(4) 사과이거나 바나나인 것이 두 개 있다. ( ∃x∃y((A(x) ∨ B(x)) ∧ (A(y) ∨ B(y)) ∧ ¬(x = y) ∧ ∀z((A(x) ∨ B(y)) → (z = x) ∨ (z = y)) )
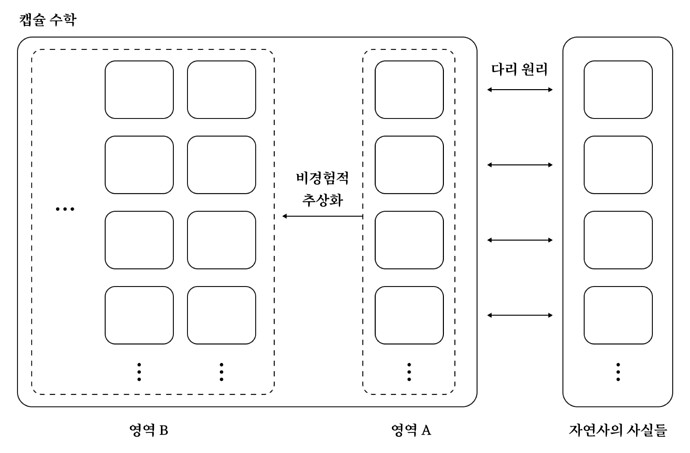
퍼트넘의 논증을 좇아 비트겐슈타인의 수학철학과 모순론을 다음과 같이 해석할 수 있다. 이해의 편의를 위하여 도표를 삽입하였다.
Gerrard(1991)가 지적했듯이 비트겐슈타인의 수학철학에서는 두 가지 논제가 반복해서 등장한다. 첫째, 수학의 명제는 경험에 의해 수정되지 않는다. 이것은 이승종 교수가 “캡슐화된 자율성”이라고 명명한 수학의 특징이며, 위의 도표에서 ‘캡슐 수학’이라는 이름으로 표시하였다. 둘째, 그럼에도 불구하고 경험, 즉 자연사의 가장 기본적인 사실들이야말로 우리의 수학적 실행에 대한 해명에서 제시할 수 있는 최종 지평이다.
[수학이] 경험에 의존하는 까닭은 사정이 달라지면 당신은 이 계산을 사용하지 않을 것이기 때문이다. 그것의 증명은 오직 그것이 경험에 유용한 결과를 주기 때문에 증명이라고 불린다. (LFM, p. 42)
두 논제는 “필연성은 우연성의 등에 업혀 있다(Tait, 2005)”는 표어로 합치한다. 이 표어에 의거하여 필연성을 주입받는 수학의 영역은 위의 도표에서 영역 A로 표시하였다.
비트겐슈타인의 모순론이 강조하는 점은 모순이 일어나는 영역이 영역 B에 국한된다는 것이다. 영역 B에서는 충분히 모순이 발생할 수 있다. 그것은 러셀의 역설과 같이 수학적 논증의 모델을 구성하는 과정에서 간과한 허점에 의해 발생할 수도 있고, 바나흐-타르스키 역설이나 톰슨의 역설과 같이 영역 B와 생활 세계를 무리하게 연결하려는 시도에 의해 발생할 수도 있다. 그러나 영역 B는 생활 세계와 유리된 공간에서 구축된 체계이기 때문에 영역 B의 모순은 다리를 건설하는 등과 같은 수학적 실행과 무관하다. 모순 및 폭발 원리가 수학적 실행에 심각한 문제를 제기한다고 생각하는 사람은 영역 A가 지니는 확실성의 원천이 영역 B에서 기원한다고 생각하기에 그러한 걱정을 하는 것이다. 그러나 실제로 영역 A가 지니는 확실성은 자연사의 사실들로부터 기원한 것이다. 따라서 영역 A는 모순의 위협에서 철저히 벗어나 있다.
3. 수학의 국소적 필연성에 관한 비판
이승종 교수는 다음과 같이 주장한다.
“수학적 실행은 경계 안쪽에서 필연적 강제력을 지닌다. (중략) [그러나] 보편성이나 독점성을 보장받지 못[한다].” (NRW, p. 225)
그러나 필자는 NRW에 제시된 논증만으로는 수학의 국소적 필연성을 개진하기에 부족하다고 본다. 왜냐하면 수학의 국소적 필연성은 다양한 수학 체계를 일관된 방식으로 설명하는, 필자가 ‘메타수학의 보편적 필연성’이라고 부르는 현상을 설명하지 못하기 때문이다.
이승종 교수가 직접 거론한 “디지털적 분절이 없는 아날로그적 액체 세계(NRW, p. 222)”를 예시로 논의해 보겠다. 이승종 교수가 명시적으로 밝히지는 않았지만 아마 그는 액체 세계의 수학으로서 실수 이론을 염두에 뒀을 것이다. 엄밀하게 진술하자면 액체 세계의 수학은 닫힌 실수체 이론 ⟨R, +, ·, 0, 1, <⟩일 것이다. 이 이론은 우리의 수학이라 부를 수 있는 페아노 산술 이론 ⟨N, 0, S⟩와 크게 다를 뿐 아니라, 타르스키-자이덴베르크 정리에 따르면 호환이 불가능하다. 실수체 이론은 결정가능한(decidable) 이론이지만, 페아노 산술 이론은 그렇지 않기 때문이다. 이승종 교수는 이를 근거로 다양한 수학 체계의 가능성과, 그러한 가능성이 시사하는 수학의 국소적 필연성을 역설하는 것으로 보인다.
그러나 다음 질문이 가능하다. 타르스키-자이덴베르크 정리는 어떤 수학 체계에 속하는 이론인가? 타르스키-자이덴베르크 정리는 실수체 이론에 관한 정리이지만, 이 정리는 우리의 세계, 즉 디지털적 분절의 세계에서도 증명할 수 있다. 말하자면, 타르스키-자이덴베르크 정리는 액체 세계와 디지털 세계 양쪽에서 보편적 지위를 인정 받는다. 이것은 메타수학적 진술이 가지는 특징이며, 수학의 필연성을 국소적인 영역에 국한하려는 모든 철학적 이론에 문제를 일으킨다. 이 문제는 프레게 또한 지적한 바 있다. 프레게가 형식주의 진영을 향해, 형식적 수학 게임에 속한 이론과는 달리 형식적 수학 게임에 관한 이론은 해당 게임에서 무엇이 가능하고 무엇이 가능하지 않은지를 진술하는 의미 있는 이론이라고 비판하였다(Frege, 1953).
이렇듯 수학은 어느 하나의 캡슐 안에만 갇혀 있을 수밖에 없는 학문이 아니다. 수학은 다른 캡슐에 관해서도 의미 있는 진술을 할 수 있을 뿐 아니라, 두 캡슐 사이에 다리를 놓기도 한다. 체르멜로-프렝켈 집합론과 폰 노이만-베르나이스-괴델 집합론이 보존적 관계에 있다는 정리가 그러한 사례라고 할 수 있다. 이토록 강력하고 유동적인 메타수학의 필연성에 관한 적절한 설명이 없다면 이승종 교수와 비트겐슈타인의 ‘수학의 국소적 필연성’ 이론은 수학자들에게 진지하게 받아들여지기 어려울 것이다.
각주
¹ ‘부합하다’라는 표현을 사용한 이유는 램프의 작동 방식이 함수 f와 정확히 일치하지는 않아도 되기 때문이다(정확히 일치하는 것은 불가능하다). 예를 들어 2kg 상자와 3kg 상자를 같이 저울에 올렸을 때 5kg으로 측정되는 사태는 2 + 3 = 5에 부합하는 사태이지만, 각각의 상자가 정확히 2kg과 3kg이지는 않다. 따라서 어떤 사태가 수학적 명제에 ‘부합’하느냐의 기준은, 후술할 ‘다리 원리’에 의해 사태와 명제가 매개될 수 있는가의 여부이다.
참고문헌
Earman, John & Norton, John (1996). Infinite pains: the trouble with supertasks. In Adam Morton & Stephen P. Stich (eds.), Benacerraf and His Critics. Blackwell. pp. 11–271.
Frege, Gottlob (1950). The Foundations of Arithmetic: A Logico-Mathematical Enquiry Into the Concept of Number. New York, NY, USA: Northwestern University Press. §93.
Garver, Newton (1996). Philosophy as grammar. In Hans D. Sluga & David G. Stern (eds.), The Cambridge Companion to Wittgenstein. Cambridge University Press. pp. 139–170.
Gerrard, Steve (1991). Wittgenstein's philosophies of mathematics. Synthese 87 (1):125-142.
Putnam, H. (1979). The thesis that mathematics is logic. In Mathematics, Matter and Method: Philosophical Papers (pp. 12-42). Cambridge: Cambridge University Press.
Tait, William. (2005). The provenance of pure reason. Essays in the philosophy of mathematics and its history. pp. 116
Thomson, James (1954). Tasks and Supertasks. Analysis 15 (1):1–13.